Kalkulatory granic to praktyczne narzędzia online do obliczania granic funkcji i ciągów. Ułatwiają one zrozumienie i rozwiązywanie problemów z analizy matematycznej. Użytkownicy mogą szybko wprowadzić funkcję, określić punkt graniczny i uzyskać wynik. To szczególnie przydatne dla uczniów i studentów.
Kalkulatory obsługują różne typy funkcji, w tym trygonometryczne i logarytmiczne. Pozwalają na obliczanie granic jednostronnych i obustronnych. Są pomocne w sprawdzaniu własnych obliczeń i radzeniu sobie z trudniejszymi przypadkami, jak granice wymagające reguły de L'Hospitala. Najważniejsze informacje:- Umożliwiają szybkie obliczanie granic funkcji i ciągów
- Wspierają różne rodzaje funkcji matematycznych
- Pozwalają na wybór rodzaju granicy (jednostronna, obustronna)
- Szczególnie przydatne w edukacji i samodzielnej nauce
- Pomagają w weryfikacji ręcznych obliczeń
- Radzą sobie z bardziej skomplikowanymi przypadkami granic
Czym jest granica ciągu matematycznego?
Granica ciągu to wartość, do której zbliżają się kolejne wyrazy ciągu, gdy numer wyrazu rośnie do nieskończoności. Określa ona zachowanie ciągu w dalekiej perspektywie.
Granice ciągów odgrywają kluczową rolę w analizie matematycznej. Umożliwiają badanie zbieżności szeregów nieskończonych. Pomagają też w zrozumieniu zachowania funkcji w punktach nieciągłości.
Oto przykłady ciągów zbieżnych i rozbieżnych:
- Ciąg zbieżny: a_n = 1/n (granica 0)
- Ciąg zbieżny: a_n = (n^2 + 1)/(n^2 + 2n) (granica 1)
- Ciąg rozbieżny: a_n = n (brak granicy)
- Ciąg rozbieżny: a_n = (-1)^n (oscyluje między -1 i 1)
Funkcjonalności kalkulatora granic ciągów online
Kalkulator granic ciągów to zaawansowane narzędzie online do szybkich obliczeń matematycznych. Umożliwia precyzyjne wyznaczanie granic różnych typów ciągów. Oferuje intuicyjny interfejs, ułatwiający wprowadzanie danych i interpretację wyników.
Narzędzie obsługuje szeroką gamę ciągów. Radzi sobie z ciągami arytmetycznymi, geometrycznymi i harmonicznymi. Potrafi analizować ciągi rekurencyjne i te zadane wzorem ogólnym. Wspiera również obliczenia dla ciągów z funkcjami trygonometrycznymi czy wykładniczymi.
Oto dodatkowe opcje kalkulatora granic:
- Obliczanie granic jednostronnych
- Analiza zbieżności ciągu
- Wyznaczanie punktów nieciągłości
- Generowanie wykresów ciągów
- Eksport wyników do różnych formatów
Czytaj więcej: Jak wypełnić oświadczenie o kolizji? Kroki i formularze wymagane po wypadku
Jak korzystać z kalkulatora granic ciągów?
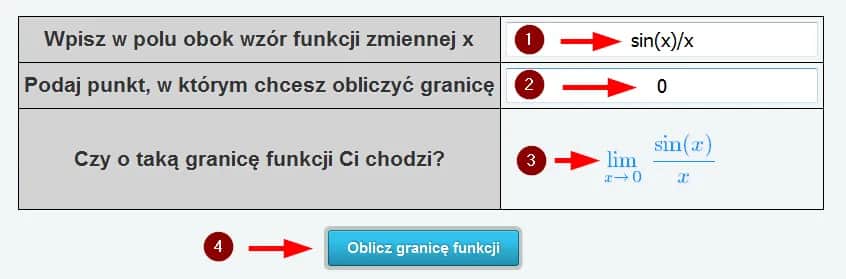
Wprowadzanie danych
Wzór ciągu wpisuje się używając standardowej notacji matematycznej. Zmienną oznaczającą numer wyrazu zazwyczaj symbolizuje "n". Można korzystać z podstawowych operatorów (+, -, *, /) oraz funkcji (sqrt, sin, ln).
Punkt graniczny to najczęściej nieskończoność. Niektóre kalkulatory granic pozwalają też na badanie granic w konkretnych punktach.
Ustawienia kalkulatora
Większość kalkulatorów granic online oferuje różnorodne opcje konfiguracji. Możesz wybrać poziom dokładności obliczeń. Niektóre narzędzia pozwalają na zmianę formatu wyniku (ułamek zwykły/dziesiętny). Zaawansowane kalkulatory granic jednostronnych umożliwiają wybór strony, z której badana jest granica.
Generowanie wyniku
Po kliknięciu przycisku "Oblicz", narzędzie do granic matematycznych rozpoczyna proces analityczny. Wynik pojawia się zazwyczaj w ciągu kilku sekund.
Otrzymany rezultat może być przedstawiony na kilka sposobów. Najczęściej to wartość liczbowa, symbol nieskończoności lub informacja o braku granicy. Niektóre kalkulatory granic niewłaściwych dostarczają dodatkowych komentarzy wyjaśniających charakter granicy.
Przykłady obliczeń różnych typów granic ciągów
Granica ciągu arytmetycznego a_n = 2n + 1 to nieskończoność. Wynika to z nieograniczonego wzrostu kolejnych wyrazów.
Granica ciągu geometrycznego a_n = (1/2)^n wynosi 0. Kolejne wyrazy zbliżają się do zera, nigdy go nie osiągając.
Granica ciągu harmonicznego a_n = 1/n również wynosi 0. Choć ciąg zbiega wolniej niż geometryczny, ostatecznie dąży do zera.
| Typ ciągu | Wzór | Granica | Interpretacja |
| Arytmetyczny | 2n + 1 | ∞ | Rozbieżny do nieskończoności |
| Geometryczny | (1/2)^n | 0 | Zbieżny do zera |
| Harmoniczny | 1/n | 0 | Zbieżny do zera (wolno) |
| Oscylacyjny | (-1)^n | Brak | Rozbieżny oscylacyjnie |
Jak interpretować wyniki z kalkulatora granic?
Wynik liczbowy oznacza, że ciąg jest zbieżny. Wartość ta wskazuje, do jakiej liczby dążą wyrazy ciągu. Im bliżej tej wartości, tym większy numer wyrazu.
Symbole +∞ lub -∞ sugerują, że ciąg rośnie lub maleje nieograniczenie. Kalkulator granic w nieskończoności często stosuje te oznaczenia.
Granice niewłaściwe to przypadki specjalne. Mogą oznaczać oscylacje ciągu lub sytuacje, gdy granica nie istnieje. Kalkulator granic niewłaściwych zazwyczaj dostarcza dodatkowych wyjaśnień dla takich przypadków.
- Sprawdź zachowanie ciągu dla dużych wartości n
- Porównaj wynik z intuicyjnym przewidywaniem
- Użyj innego kalkulatora granic online do weryfikacji
Kalkulator granic vs. obliczenia ręczne
Zalety korzystania z kalkulatora
Czas to pieniądz! Kalkulator granic ciągów błyskawicznie generuje wyniki. Eliminuje żmudne obliczenia, oszczędzając cenne minuty.
Precyzja na najwyższym poziomie. Narzędzie do granic matematycznych minimalizuje ryzyko błędów obliczeniowych. Zapewnia dokładność nawet przy skomplikowanych ciągach.
Złożone ciągi? Żaden problem! Kalkulator granic radzi sobie z zaawansowanymi wyrażeniami. Analizuje ciągi z funkcjami wykładniczymi, logarytmicznymi czy trygonometrycznymi. Umożliwia badanie granic, które ręcznie byłyby trudne do obliczenia.
Kiedy warto liczyć ręcznie?
Zrozumienie to podstawa! Ręczne obliczenia pomagają głębiej pojąć koncepcję granic. Krok po kroku analizujesz zachowanie ciągu. To buduje intuicję matematyczną i utrwala wiedzę.
Egzaminy za pasem? Ćwicz ręczne obliczenia! Większość testów nie pozwala na korzystanie z kalkulatorów granic online.
Ograniczenia kalkulatorów online do obliczania granic
Uwaga na nietypowe ciągi! Niektóre kalkulatory granic mogą mieć problem z analizą bardzo specyficznych sekwencji. Ciągi z niestandardowymi funkcjami czy skomplikowanymi rekurencjami bywają wyzwaniem. W takich przypadkach warto porównać wyniki z kilku źródeł.
Gigantyczne liczby to pułapka. Przy ekstremalnie dużych wartościach możliwe są niedokładności. Ograniczenia pamięci i precyzji obliczeń mogą wpływać na wynik.
Brak internetu? No limits! Obliczanie granic online wymaga połączenia sieciowego. W krytycznych momentach może to być problemem.
Najlepsze kalkulatory granic ciągów dostępne w sieci
WolframAlpha to potężne narzędzie analityczne. Oferuje zaawansowane obliczanie granic online. Dostarcza szczegółowe wyjaśnienia kroków. Generuje wykresy dla lepszej wizualizacji.
Symbolab to przyjazny użytkownikowi kalkulator granic. Obsługuje szeroki zakres funkcji matematycznych. Umożliwia krokowe rozwiązywanie problemów. Oferuje mobilną aplikację dla wygody użytkowania.
Mathway to wszechstronne narzędzie edukacyjne. Wspiera obliczanie granic jednostronnych. Zapewnia wskazówki do samodzielnego rozwiązywania zadań. Integruje się z innymi działami matematyki dla kompleksowej analizy.
| Funkcja | WolframAlpha | Symbolab | Mathway |
| Obliczanie granic | ✓ | ✓ | ✓ |
| Granice jednostronne | ✓ | ✓ | ✓ |
| Wykresy | ✓ | ✓ | ✓ |
| Krokowe rozwiązania | ✓ | ✓ | ✓ |
| Aplikacja mobilna | ✓ | ✓ | ✓ |
Kalkulatory granic ciągów: Narzędzia przyspieszające analizę matematyczną
Kalkulatory granic ciągów to potężne narzędzia online, które rewolucjonizują sposób, w jaki podchodzimy do obliczeń matematycznych. Oferują szybkość, precyzję i wszechstronność w analizie różnorodnych ciągów - od prostych arytmetycznych po złożone funkcje wykładnicze czy trygonometryczne.
Choć obliczanie granic online ma swoje niezaprzeczalne zalety, warto pamiętać o równowadze między wykorzystaniem technologii a rozwijaniem własnych umiejętności matematycznych. Ręczne obliczenia nadal mają swoją wartość, szczególnie w kontekście edukacyjnym i egzaminacyjnym.
Wybierając kalkulator granic, warto zwrócić uwagę na takie funkcje jak obsługa granic jednostronnych, generowanie wykresów czy możliwość krokowego rozwiązywania problemów. Narzędzia takie jak WolframAlpha, Symbolab czy Mathway oferują zaawansowane możliwości, które mogą znacząco ułatwić pracę z granicami ciągów.