Granice ciągu i kalkulatory limitów to ważne narzędzia w analizie matematycznej. Pomagają zrozumieć, do jakiej wartości zbliża się funkcja lub ciąg. Kalkulatory online ułatwiają obliczanie tych granic. Są szybkie i dokładne. Pokazują też kroki rozwiązania, co pomaga w nauce.
Kalkulatory limitów pozwalają wprowadzić funkcję, określić punkt i rodzaj granicy. Obsługują różne typy funkcji, w tym trygonometryczne i logarytmiczne. Mogą też korzystać z reguły de L'Hospitala dla trudniejszych przypadków.
Najważniejsze informacje:- Kalkulatory limitów przyspieszają obliczenia matematyczne
- Umożliwiają obliczanie granic jednostronnych i obustronnych
- Prezentują szczegółowe kroki rozwiązania
- Obsługują różne typy funkcji matematycznych
- Pomagają w nauce i zrozumieniu koncepcji granic
Czym jest granica ciągu?
Granica ciągu to wartość, do której zmierzają kolejne wyrazy ciągu, gdy numer wyrazu dąży do nieskończoności. Innymi słowy, to punkt, wokół którego skupiają się elementy ciągu w miarę jego rozwoju.
Znaczenie granic ciągów w matematyce jest ogromne. Stanowią one fundament analizy matematycznej, umożliwiając badanie zachowania funkcji w nieskończoności. Granice ciągów pomagają również w zrozumieniu koncepcji ciągłości i różniczkowalności funkcji.Oto 3 najważniejsze zastosowania granic ciągów:
- Analiza zachowania funkcji w punktach nieciągłości
- Badanie zbieżności szeregów nieskończonych
- Definiowanie pochodnych i całek w analizie matematycznej
Jak działa kalkulator granic ciągu?
Kalkulator granic ciągu to narzędzie online, które automatyzuje proces obliczania granic. Umożliwia wprowadzenie wzoru ciągu, określenie punktu granicznego oraz wybór rodzaju granicy. Kalkulator analizuje dane wejściowe, przeprowadza obliczenia i prezentuje wynik. Dodatkowo, wiele kalkulatorów pokazuje kroki rozwiązania, co jest niezwykle pomocne w nauce.
Oto instrukcja krok po kroku, jak korzystać z kalkulatora granic ciągu:
- Wejdź na stronę z kalkulatorem granic
- Wprowadź wzór ciągu w odpowiednie pole
- Określ punkt graniczny (np. nieskończoność lub konkretna wartość)
- Wybierz rodzaj granicy (jednostronna, obustronna)
- Kliknij przycisk "Oblicz" i odczytaj wynik
Czytaj więcej: Jakie są odpowiedzi z egzaminu z matematyki 2023? Przykładowe odpowiedzi
Rodzaje granic ciągów obsługiwane przez kalkulatory online
Granice jednostronne
Granice jednostronne to limity funkcji, gdy zbliżamy się do punktu tylko z jednej strony. Mogą być lewostronne (gdy zbliżamy się od mniejszych wartości) lub prawostronne (gdy zbliżamy się od większych wartości).
Przykład obliczenia: Dla funkcji f(x) = (x^2 - 1) / (x - 1), granica jednostronna prawa w punkcie x = 1 wynosi 2. Kalkulator granic wykonuje to obliczenie, analizując zachowanie funkcji dla wartości x nieznacznie większych od 1.
Granice obustronne
Granice obustronne uwzględniają zbliżanie się do punktu z obu stron jednocześnie. Są kluczowe dla badania ciągłości funkcji.
Przykładowe obliczenie: Dla funkcji g(x) = sin(x) / x, granica obustronna w punkcie x = 0 wynosi 1. Kalkulator granic funkcji wykonuje to obliczenie, badając zachowanie funkcji dla wartości x zbliżających się do 0 zarówno od strony dodatniej, jak i ujemnej.
Granice niewłaściwe
Granice niewłaściwe odnoszą się do sytuacji, gdy wartość funkcji dąży do nieskończoności lub gdy argument funkcji zmierza do nieskończoności. Są kluczowe w analizie funkcji wykładniczych i logarytmicznych.
Przykład z użyciem kalkulatora: Dla funkcji h(x) = e^x, granica niewłaściwa gdy x dąży do nieskończoności, również wynosi nieskończoność. Kalkulator granic niewłaściwych poradzi sobie z tym obliczeniem, analizując zachowanie funkcji dla bardzo dużych wartości x.
Przykłady obliczeń z użyciem kalkulatora granic ciągu
Przykład 1: Prosty ciąg arytmetyczny a_n = 2n + 1. Kalkulator granic ciągu pokaże, że granica tego ciągu, gdy n dąży do nieskończoności, to nieskończoność. Narzędzie analizuje wzór, zauważa liniowy wzrost i określa brak górnego ograniczenia.
Przykład 2: Ciąg geometryczny b_n = (1/2)^n. Obliczanie granic ciągu dla tego przypadku wykaże, że granica wynosi 0. Kalkulator rozpoznaje malejący charakter ciągu i zbieżność do zera.
Przykład 3: Ciąg z funkcją trygonometryczną c_n = sin(n)/n. Narzędzie do granic matematycznych obliczy, że granica tego ciągu to 0. Analizuje ono oscylacje sinusa i dzielenie przez rosnące n.
Najpopularniejsze kalkulatory granic ciągu online
| Nazwa | Główne cechy | Łatwość użycia |
|---|---|---|
| WolframAlpha | Zaawansowane obliczenia, szczegółowe kroki | Średnia |
| Symbolab | Intuicyjny interfejs, wsparcie dla różnych typów granic | Wysoka |
| Mathway | Proste obliczenia, szybkie wyniki | Bardzo wysoka |
Rekomendujemy Symbolab jako najlepszy kalkulator granic ciągu. Łączy on zaawansowane funkcje z przyjaznym interfejsem, co czyni go idealnym dla większości użytkowników.
Jak uniknąć błędów przy korzystaniu z kalkulatora granic?
- Błąd: Niepoprawne wprowadzenie wzoru - Rozwiązanie: Dokładnie sprawdź składnię
- Błąd: Wybór niewłaściwego typu granicy - Rozwiązanie: Upewnij się, czy potrzebujesz granicy jednostronnej czy obustronnej
- Błąd: Ignorowanie warunków istnienia funkcji - Rozwiązanie: Zawsze analizuj dziedzinę funkcji
- Błąd: Błędna interpretacja wyników - Rozwiązanie: Zapoznaj się z notacją używaną przez kalkulator
Interpretacja wyników z kalkulatora granic ciągu
Kalkulator granic ciągu może zwrócić różne typy wyników. Może to być konkretna liczba, symbol nieskończoności, lub informacja o braku granicy. Zrozumienie tych wyników jest kluczowe dla prawidłowej interpretacji zachowania ciągu.
Co oznacza wynik "nieskończoność"?
Wynik "nieskończoność" wskazuje, że wartości ciągu rosną bez ograniczenia. Oznacza to, że ciąg nie jest ograniczony z góry. Dla przykładu, ciąg a_n = n^2 ma granicę równą nieskończoności.
Jak rozumieć wynik "granica nie istnieje"?
Wynik "granica nie istnieje" pojawia się, gdy ciąg nie zbieguje się do żadnej konkretnej wartości. Może to oznaczać, że ciąg oscyluje między różnymi wartościami lub rozbiega się w różnych kierunkach. Przykładem może być ciąg b_n = (-1)^n, który na przemian przyjmuje wartości 1 i -1.
Zaawansowane funkcje kalkulatorów granic ciągu
Obliczanie granic w punkcie umożliwia badanie zachowania funkcji w okolicy konkretnej wartości. Limity funkcji online często oferują analizę granic jednostronnych. Funkcja obliczania granic niewłaściwych pozwala badać zachowanie funkcji dla bardzo dużych wartości argumentu.
Przykład wykorzystania zaawansowanej funkcji: Użyjmy kalkulatora granic niewłaściwych do zbadania funkcji f(x) = ln(x)/x gdy x dąży do nieskończoności. Kalkulator wykaże, że granica wynosi 0, analizując zachowanie logarytmu i funkcji liniowej dla bardzo dużych wartości x.
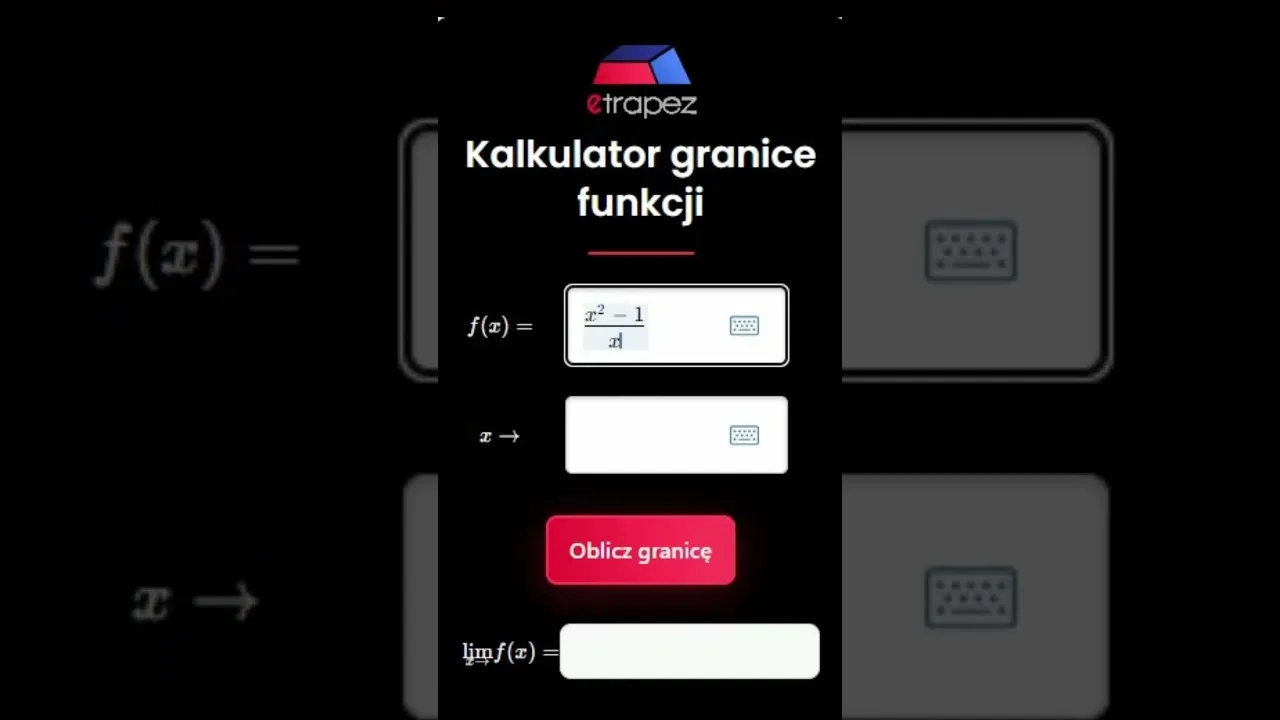
Dlaczego warto korzystać z kalkulatora granic ciągu?
- Oszczędność czasu przy skomplikowanych obliczeniach
- Minimalizacja ryzyka błędów obliczeniowych
- Możliwość weryfikacji ręcznych obliczeń
- Pomoc w zrozumieniu koncepcji granic poprzez analizę kroków rozwiązania
- Możliwość szybkiego eksperymentowania z różnymi ciągami i funkcjami
Kalkulatory granic ciągu to nieocenione narzędzia w nauce i pracy z matematyką. Łączą szybkość obliczeń z edukacyjnym aspektem prezentacji kroków rozwiązania, co czyni je idealnymi zarówno dla uczniów, jak i profesjonalistów.
Odkryj moc kalkulatorów granic ciągu
Kalkulatory granic ciągu to potężne narzędzia, które rewolucjonizują sposób, w jaki podchodzimy do obliczeń matematycznych. Dzięki nim, skomplikowane zadania stają się proste i dostępne dla każdego. Niezależnie od tego, czy jesteś studentem, nauczycielem czy profesjonalistą, te narzędzia oferują niezrównaną precyzję i szybkość w analizie zachowań funkcji i ciągów.
Pamiętaj, że granice funkcji to nie tylko suche wzory - to klucz do zrozumienia dynamiki świata matematycznego. Dzięki kalkulatorom online możesz eksplorować różne typy granic, od jednostronnych po niewłaściwe, z łatwością i pewnością. To jak mieć osobistego matematycznego eksperta na wyciągnięcie ręki!
Wykorzystaj potencjał tych narzędzi, aby pogłębić swoją wiedzę, oszczędzić czas i uniknąć błędów. Obliczanie granic ciągu nigdy nie było tak przystępne. Pamiętaj jednak, aby zawsze krytycznie analizować wyniki i wykorzystywać kalkulatory jako wsparcie, a nie zastępstwo dla zrozumienia koncepcji matematycznych. Z tymi narzędziami, świat granic i funkcji stoi przed tobą otworem!